Analisi della distribuzione

Anche limitandosi ai parti naturali, la scelta dell'ospedale (e quindi il rientrare o meno nella casistica esaminata) dipende da fattori esterni. Per verificare la possibilità che fattori di questo tipo inquinino i dati, si è effettuato un'analisi della distribuzione del numero di nati.

In teoria, ci si aspetta che la distribuzione delle nascite, in quanto eventi indipendenti e scorrelati tra di loro, segua una statistica poissoniana. Questa distribuzione è caratterizzata in modo univoco dalla probabilità individuale di avere una nascita in un giorno quasiasi, che può essere stimata direttamente dal numero medio di nascite giornaliere nel periodo in esame.

Analizzando in questo modo i dati disponibili si vede immediatamente che la distribuzione osservata differisce notevolmente da una poissoniana. In particolare, esiste un numero elevato di giorni in cui si hanno pochissime o moltissime nascite, mentre accade più raramente di quanto ci si aspetterebbe di avere un numero di nascite "medio" (fig. 3a). La distribuzione ha un valore di $\chi^2=33$, P < 0.0001.

Andando a verificare quali siano i giorni con un numero di nascite fuori statistica, si nota come questi siano tipicamente molto raggruppati. In particolare, la quasi totalità dei giorni con poche nascite sono concentrati tra il 13 Novembre e il 20 Dicembre 1979. I giorni con un eccesso di natalità sono compresi tra il 15 e il 23 Ottobre 1978. Il primo periodo coincide con un periodo di chiusura del reparto maternità di Careggi, mentre il secondo probabilmente è legato alla chiusura di un ospedale in un comune limitrofo. Un ulteriore periodo spurio è costituito dagli ultimi giorni in esame, che probabilmente non contengono una registrazione completa dei nati.

Nella successiva analisi dei dati, questi tre periodi sono stati eliminati in quanto riconducibili ad eventi esterni che non c'entrano con la Luna. E' comunque interessante notare come i dati esclusi, essendo molto concentrati nel tempo, generano un grosso picco (25 nati al giorno in più, per un eccesso complessivo di 80 nati) in corrispondenza dell'inizio della luna calante. Pertanto anche un singolo evento esterno può generare un picco significativo nei dati.

Eliminando questi tre periodi, la distribuzione resta significativamente non poissoniana, ma il valore di $\chi^2$ scende da 30 a 3.7 (fig. 3b). L'allargamento della distribuzione dipende in buona parte dalla significativa variazione della natalità negli anni in esame (da 8.7 a 7.0 nati/giorno) (fig. 2). Infatti, dividendo il periodo considerato in 3 parti, ciascun sottoperiodo mostra una distribuzione quasi poissoniana, ma con media significativamente differente. Non si è quindi cercato ulteriori fattori confondenti.

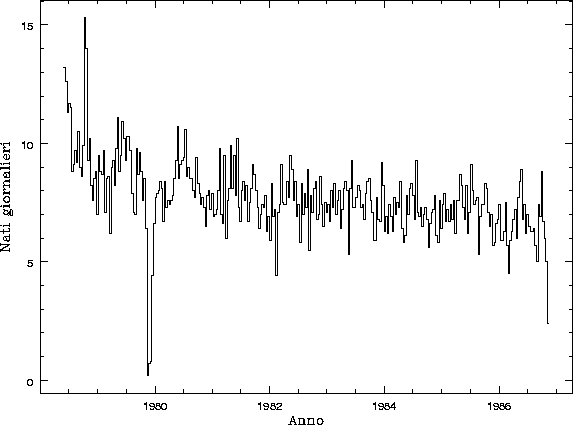
Fig. 2: Nati giornalieri nel periodo in esame

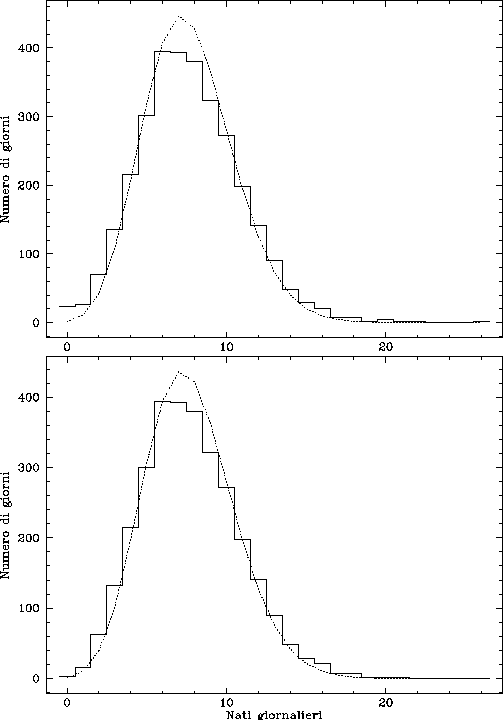
Fig. 3: Distribuzione del numero dei nati, con (sopra) e senza (sotto) i due periodi anomali visibili in fig. 2.